Dessiner en perspective
Il s'agit ici de (re?) découvrir les bases, mais aussi les trucs et astuces, qui nous permettent de faire moins d'erreurs avec la perspective.
La perspective fait partie des techniques de base du dessin, et c'est pourquoi elle est souvent enseignée aux débutants. Elle consiste en quelques règles de projection de la réalité tri-dimensionnelle sur le plan de notre feuille.
Sommaire
 |
Toutes les lignes verticales restent verticales. (Sauf cas rare de la contre plongé) |
|
Les lignes horizontales convergent en un ou plusieurs points sur la ligne d'horizon. |
|
Les lignes qui ne sont pas horizontales convergent au dessus ou au dessous de l'horizon. |
|
Toutes les paralléles convergent en un même point. |
 |
Tout ce qui se trouve à hauteur de la ligne d'horizon est à la hauteur de l'observateur. Donc si l'observateur à ses yeux à 1,70 m, quelque soit le point de départ, n'importe quel piquet qui se finit sur la ligne d'horizon mesure 1,70m. Lire aussi Comprendre et situer la ligne d'horizon |
Cube à la perspective exagérée.
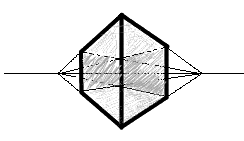
On voit ici deux points de fuites sur l'horizon. Les parallèles convergent toutes vers le même point.
Des mesures peuvent être prises pour toutes les lignes verticales ou horizontales, par rapport à la hauteur de l'horizon.
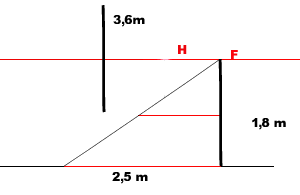
Ici l'horizon est à 1,8m de hauteur. Donc tous les éléments posés au sol qui touchent l'horizon mesurent 1,8 m. Le piquet de gauche, qui est aussi grand au dessus qu'en dessous de l'horizon mesure donc 3,6 mètres. Par rapport au piquet de droite, nous pouvons aussi déterminer la largeur de la route, approximativement 2m50. Les deux lignes rouges horizontales figurent toutes les deux 2m50.
Les ellipses sont plus faciles à construire si l'on considère qu'elles s'inscrivent dans un rectangle. Le centre se trouve à l'intersection des diagonales. Il ne reste plus alors à dessiner approximativement une ellipse en restant tangeant au rectangle.
 |
Le verre ci contre est un exemple de perspective inexacte fait à main levée. L'horizon est au dessus du verre, et le pied devrait donc être plus "ouvert" que le dessus du verre. Un peu plus large donc. L'utilisation de ligne de fuite permettrait d'améliorer ce dessin. Dans les bons points, les ellipses sont bien horizontales. | |
 |
Cette photographie montre comment le verre aurait du être dessiné. Mais, forcément, c'est plutôt facile à dire.... Pour s'aider il faut construire l'ellipse... |
|
 |
Construire l'ellipse | |
Les reflets apparaissent compliqués à première vue, mais finalement, il n'en est rien. Une erreur fréquente est de considérer que le reflet est l'image de l'original en sens inverse. En fait, il suffit de tracer une ligne verticale entre le point que l'on veut projeter et la surface de l'eau. On trace alors un trait de même longueur sous la surface de l'eau.
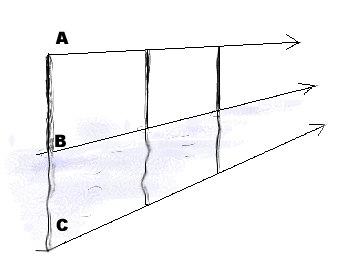
On a AB = BC. Par extension on peut calculer les reflets par rapport à des miroirs. La, la ligne n'est pas verticale, mais perpendiculaire au miroir.
Exemples : construire un carrelage
| La principale difficulté lors du dessin d'un carrelage est de déterminer la longueur des carreaux. Il existe cependant une technique simple : | |
 |
On voit ici comment construire un carrelage par divisions successives. |
| A l'aide des diagonales on détermine la moitié de la zone à carreler. Puis on recommence en divisant autant de fois que nécessaire. Si les carreaux sont carrés, ont peut aussi utiliser la diagonale de chaque carreau comme moyen de trouver le suivant. | |
Les ombres ont même point de fuite que l'objet qui les projette. Pour déterminer les ombres, il faut tracer une ligne entre la surface sur laquelle se projette l'ombre et le soleil.
L'iilustration ci dessus suppose un soleil situé à 45 degrés, et à gauche de l'image. On détermine les points de projection de l'ombre au sol avec des lignes de 45°.
Exemple : construire une clôture en perspective
| Supposons que l'on veuille dessiner une clôture dont les poteaux, de même taille sont tous situés a même distance les uns des autres. Il suffit des poser les deux premiers puis de procéder comme suit |
 |
|
Pour déterminer la position du troisième poteau, on trace une ligne passant par le sommet du premier, A et le milieu du deuxième N. On en déduit la position de F, base du troisième. On remonte à la verticale et on en déduit la heuteur du poteau. On observera aussi comment l'ombre des poteaux est construite. Ces ombres sont déterminées par rapport à l'intersection entre la ligne passant entre le sommet du poteau et le soleil et la ligne passant par O et la bas du poteau. |
En savoir plus...
Idée lecture ...
Un bon livre pas très cher pour s'initier et apprendre les fondamentaux. Permet aux plus expérimentés de réviser.
La perspective pas à pasUn livre plus cher, mais nettement plus complet, pour approfondir le sujet avec des pas à pas fort bien réalisés. Comment devenir bon en dessin d'architecture.
Liens externes ...
- Cubix est un outil pédagogique en français qui permet de faciliter l'apprentissage du dessin perspectif. L'utilisation de flash et de liens dans le texte permet d'avoir une illustration du propos qui facilite la compréhension.
Amélioré en Octobre 2019
